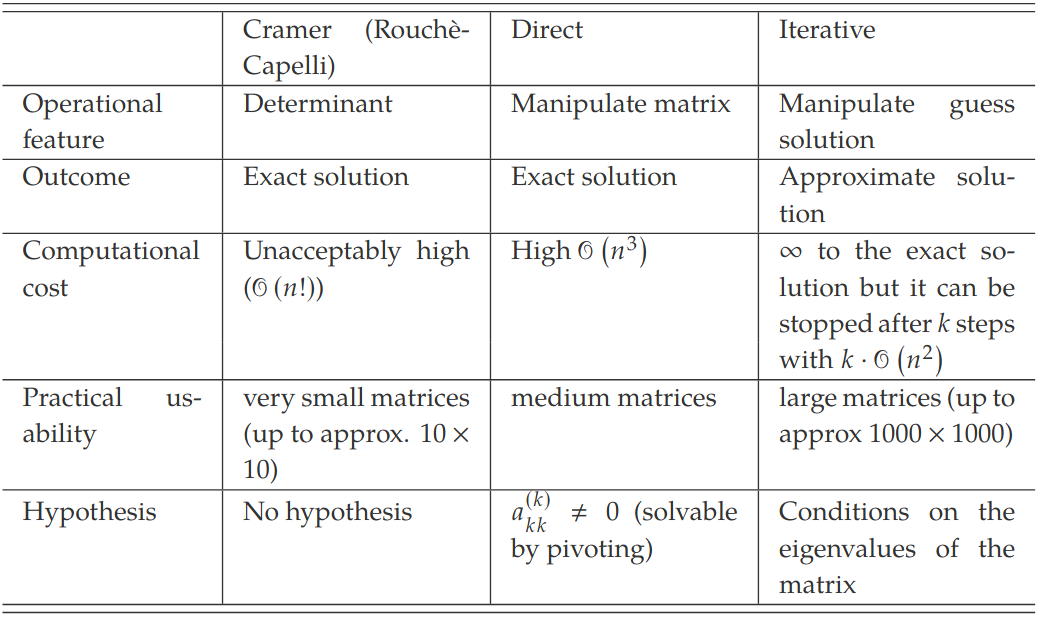
22.03.09 - Direct Methods

Cramers Method requires the calculation of 1 determinant of a $n$ order matrix and $n$ determinate of $n$ order matrices
Means $n!+n(n!)$ elementary operations
Need to find alternative methods as takes too long

Theoretical Foundations of Direct Methods

Elementary Row Operations

$E_1$ : Swap of two rows $a_i$ and $a_j$ $a_i \leftarrow a_j$ $a_j \leftarrow a_i$
$E_2$ : Multiplication of a row $a_i$ by a scalar $\lambda\in\R$ $a_i\leftarrow\lambda a_i$
$E_3$ : Substitution of a row $a_i$ by the sum of the row $a_i$ to another row $a_j$ : $a_i\leftarrow a_i+a_j$

Equivalent Matrices and Equivalent Systems

Equivalent Matrices: Apply the elementary row operations on $A$ , obtain new matrix $C\in\R_{m,n}$ .

Equivalent Systems: 2 systems of linear equations in the same variables: $Ax=b$ and $Cx=d$ . These two systems are equivalent if they have the same solutions

Consider a system of $m$ linear equations in $n$ variables $Ax=b$ . Let $A^c\in\R_{m,n+1}$ be the complete matrix associated with this system. If another system of linear equations is associated with a complete matrix $A^{'c}\in\R_{m,n+1}$ equivalent to $A^c$ , then the two systems are equivalent

$E_1$ : The swap of two rows, the equations of the system are swapped, no effect on the solution of the system
$E_2$ : Same solutions, modified systems is equivalent to the original one
$E_3$ : After operation, the modified system is equivalent in solutions to the original one

Direct Methods

Direct methods are methods for solving systems of linear equations by manipulating the original matrix to produce an equivalent system that can be easily solved. A typical manipulation is the transformation of a system of linear equation into triangular system

Gaussian Elimination

$Ax=b$

Construct the complete matrix $A^c$
Apply the elementary row operations to obtain a staircase complete matrix and triangular incomplete matrix, that is we add rows to obtain a null element in the desired position
Write down the new system of linear equations
Solve the $n^{th}$ equations of the system and use the result to solve the $(n-1)^{th}$
Continue recursively until the first equation

To obtain the matrix would do: $r^{(2)}_2=r^{(1)}_2+(\frac{-a^{(1)}_{2,1}}{a^{(1)}_{1,1}})\times r^{(1)}_1$ As it keeps going on, it gets longer and longer, to create a matrices with leading zeros

Dan Method: $a_{n,m}-(a_{n,1}\times a_{n-1,m})$ This completes the first 2 rows and first column. Then have to increase m, to do second column

LU factorisation

Direct method that transforms a Matrix into a matrix product $LU$ where $L$ is a lower triangular matrix having the diagonal elements all equal to 1 and $U$ is an upper triangular matrix $Ax=b\Rightarrow LUx=b$ Pose $Ux=y$ solve at first the triangular system $Ly=b$ and then extract $x$ from the triangular system $Ux=y$ Does not alter the vector of known terms $b$ .

If working with non singular matrix, then split any matrix into a product such that $A=LU$ . If non-singular matrix and is square, and has det of 0, then $\exists!$ lower traingular matrix $L$ having all the diagonal elements equal to 1 and $\exists!$ upper triangular matrix $U$ such that $A=LU$

Equivalence of Gaussian elimination and LU factorisation

Gaussian elimination and LU factorisation are both direct methods
They are not identical but they are equivalent
Whilst performing the algorithm the LU factorisation is implicitly performed
Both Gaussian elimination and LU factorisation have a lower complexity than theoretical methods
The complexity is in the order of $n^3$ operations

Short introduction to Iterative Methods

Jacobi's Method - Starts from an initial guess $x^{(0)}$ , iteratively apply some formulas to detect the solution of the system. Unlike direct methods that converge to the theoretical solution in a finite time, iterative methods are approximate since they converge, under some conditions